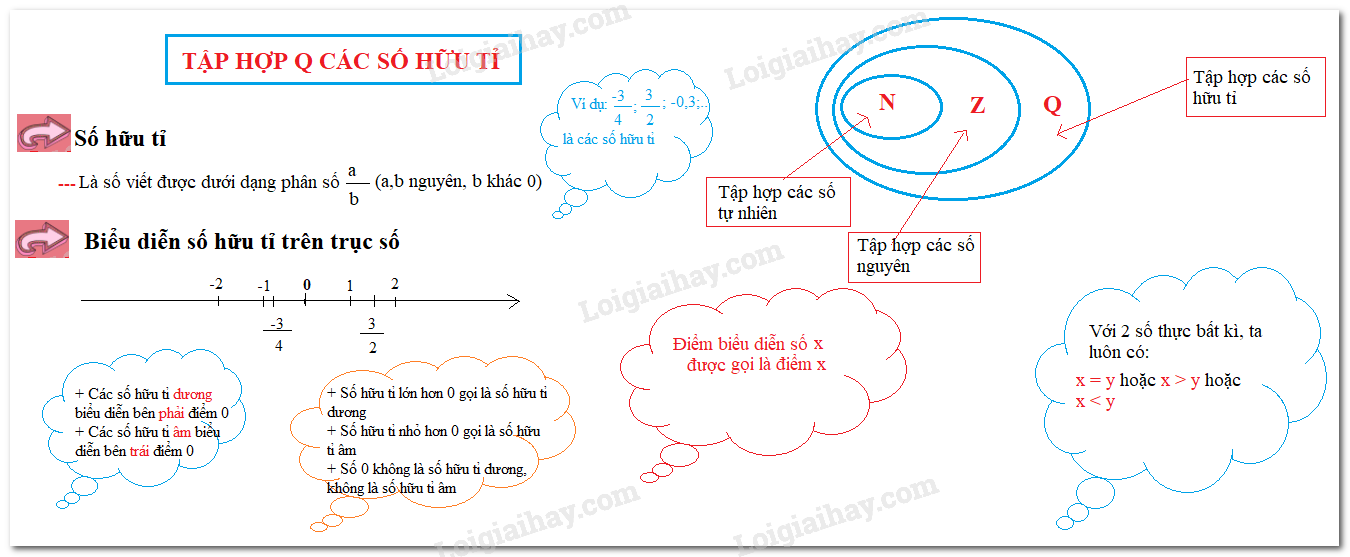
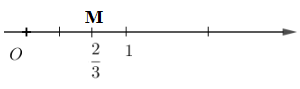1. Số hữu tỉ
Số hữu tỉ là số hoàn toàn có thể ghi chép bên dưới dạng \(\dfrac{a}{b}\) với \(a, b ∈ \mathbb Z, b \ne 0\) và tụ tập những số hữu tỉ được kí hiệu là \(\mathbb Q\)
Ví dụ: Các số \(5;\dfrac{{ - 1}}{2};\dfrac{2}{3};...\) là những số hữu tỉ
2. Biểu biểu diễn số hữu tỉ bên trên trục số
Mỗi số hữu tỉ được màn trình diễn vì thế một điểm bên trên trục số và ko tùy thuộc vào cơ hội lựa chọn phân số xác lập nó.
Ví dụ: Số hữu tỉ \(\dfrac{2}3\) được màn trình diễn vì thế điểm M bên trên trục số sau:
3. So sánh số hữu tỉ
Để đối chiếu nhị số hữu tỉ \(x,y\) tớ thực hiện như sau:
- Viết \(x,y\) bên dưới dạng phân số nằm trong khuôn dương.
\(x = \dfrac{a}{m} ; nó = \dfrac{b}{m} ( m>0)\)
- So sánh những tử là số vẹn toàn \(a\) và \(b\)
Nếu \(a> b\) thì \(x > y\)
Nếu \(a = b\) thì \(x=y\)
Nếu \(a < b\) thì \(x < y\).
Ví dụ: So sánh nhị số \(x = \frac{2}{{ - 5}}\) và \(y = \frac{{ - 3}}{{13}}\)
Ta với \(x = \frac{2}{{ - 5}} = \frac{{2.\left( { - 13} \right)}}{{\left( { - 5} \right).\left( { - 13} \right)}} = \frac{{ - 26}}{{65}}\) và \(y = \frac{{ - 3}}{{13}} = \frac{{ - 3.5}}{{13.5}} = \frac{{ - 15}}{{65}}\)
Mà \( - 26 < - 15 \Rightarrow \frac{{ - 26}}{{65}} < \frac{{ - 15}}{{65}}\) hoặc \(x < y\)
4. Chú ý
- Số hữu tỉ to hơn \(0\) gọi là số hữu tỉ dương, và được màn trình diễn vì thế những điểm ở bên phải gốc O bên trên trục số
- Số hữu tỉ nhỏ rộng lớn \(0\) gọi là số hữu tỉ âm, và được màn trình diễn vì thế những điểm phía bên trái gốc O bên trên trục số
- Số \(0\) ko là số hữu tỉ dương, cũng ko là số hữu tỉ âm
Loigiaihay.com